ゴム弾性
ゴム弾性とは、外部から与えられた力によって変形した固体物質が、高い内部応力によって瞬時に原型に復元される性質を指し、熱力学的にはエントロピー弾性と呼ばれています。全ての固体物質には弾性が有り、弾性ひずみ限界が存在します。固体物質は弾性ひずみ限界内であれば変形させても元の形状に復元しますが、この限界を超えた力が加えられると破壊されてしまいます。弾性ひずみ限界は、一般的な金属やガラスであれば最大10%程度であり、樹脂等でも50%程度ですが、ゴムは100%以上を有しており、他とは大きく異なる弾性を持つ固体物質であるということが出来ます。Oリングのシール機能は、その大半をゴム弾性に拠っています。
>>>Oリングの物性
ゴムは、以下のような特徴によって高い伸縮性を得ています。
- 長い鎖状の分子を持っている。
- 分子鎖の屈曲性が高い。
- 分子運動が液体レベルの活発な状態(分子間の結合力が弱い状態)である。
但しこの条件だけでは、伸縮性には優れていても瞬時に復元することはできません。高い復元力を得る為には、架橋によって更に分子鎖同士を結んで網目構造を形成する必要があります。ゴムは、未架橋の状態でも他の物質より大きい弾性ひずみ限界を有していますが、これを架橋することで更に大きな弾性ひずみ限界と高い復元力が生み出され、ゴム弾性を得るに至ります。
ゴムの弾性応力
ゴムの弾性変形は、非常に特異な現象です。力学的に1つの理論だけで説いていくことが出来ないこの現象は、大きく分けて微小変形領域と大変形領域という2つの領域に分けて説明することが可能です。
① 微小変形領域
ゴムを小さく変形させる領域では、「A) 伸長(圧縮)と収縮(膨張)」、「B) せん断」という2つの側面から、応力を解析します。
A) 伸長と収縮
伸長と収縮(伸縮)とは、ゴムを1本の高分子鎖と捉えると、分子鎖が自由回転することで変形を生じていると言い換えることが出来ます。
自由回転による分子鎖伸縮のイメージ図
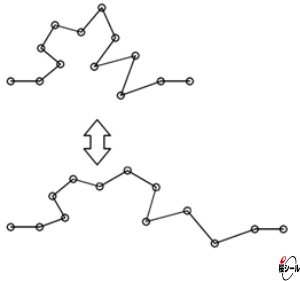
つまり、応力と歪みを線形で表せることからフックの法則を適用することが可能で、応力σと歪みεは、次の関係となります。尚、この法則がばねに用いられる場合はEをばね定数と呼びますが、ゴムの場合にはヤング率(縦弾性係数)と呼び替えます。
σ=Eε
フックの法則は伸長方向に対して成り立ちますが、伸長方向と垂直の方向では収縮が発生しているので成り立ちません。この収縮率νは、伸長側の歪みをε、収縮側の歪みε´とすると、次の関係となります。
ν=ε/ε´
この収縮率νは一般的にポアソン比と呼ばれ、物質の弾性を決定付ける最も重要な定数です。
B) せん断
横からの応力により角度を伴う変形が生じることをせん断といいます。
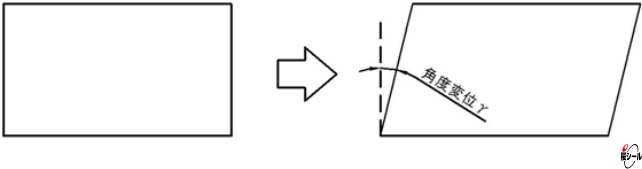
せん断変形でもフックの法則が成り立ち、せん断応力をσs、角度変位をγとすると次の関係となり、定数Gをせん断弾性率(剛性率)と呼びます。
σs=Gγ
また定数Gは、ヤング率Eとポアソンνのと間に次のような関係が成立します。
G=E/2 (1+ν)
尚、各係数はゴム材質の種類や温度、更には配合によっても変化し、おおよその値は下記の通りです。
ヤング率E : 0.01〜0.3
② 大変形領域
ゴムを大きく変形させる領域では、微小変形領域で述べた分子鎖だけでなく、架橋による網目構造の伸縮が与える影響が非常に大きくなります。この領域での変形は非線形であり、定数による1つの式で解析をすることができません。大変形領域に於けるゴムの応力曲線は下記のようになり、応力σ、歪み率λの関係です。
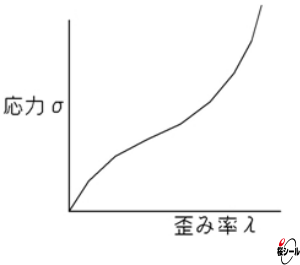
この2つから得られるエネルギー密度関数ωが重要な要素となり、次のような式を元にして弾性応力を解析することが可能です。
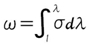
但し、非線形であることから1つの式で弾性応力を導き出すことは難しく、1つの応力をxyzの3次元方向に分割し、それぞれの方向に生じる応力として導き出すことになります。それぞれの応力をσx、σy、σz、歪み率をλx、λy、λzとした場合、ωは微分形式で表すと次にようになります。
dω=σxdλx+σydλy+σzdλz
従って、それぞれの応力は次のように表されます。
σx=∂ω/∂λx
σy=∂ω/∂λy
σz=∂ω/∂λz
三次元の応力を合わせたエネルギー密度関数ωは、応力σを用いずに表すことも可能です。ω=ω(I1、I2、I3)と表され、I1、I2、I3は3つの歪み不変量と呼ばれ、下記の式で表されます。
I1=λx²+λy²+λz²
I2=λx²λy²+λy²λz²+λz²λx²
I3=λx²λy²λz²
以上を元に各応力の式を整理したものが以下の通りで、これらが各方向の弾性応力値です。
σx=2λx{∂ω/∂I1+∂ω/∂I2(λy²+λz²)+∂ω/∂I3(λyλz)²}
σy=2λy{∂ω/∂I1+∂ω/∂I2(λx²+λz²)+∂ω/∂I3(λxλz)²}
σz=2λz{∂ω/∂I1+∂ω/∂I2(λy²+λx²)+∂ω/∂I3(λyλx)²}
このように、大変形領域ではxyzの各方向に分解した弾性応力が算出されます。
以上が2つの領域から成るゴム弾性変形の解析です。しかし実際には大変形領域にも微小変形領域の要素が含まれ、また温度による数値変化も多分に発生します。ゴムの弾性応力は解析するのが非常に困難です。
桜シール株式会社
住所
〒130-0021
東京都墨田区緑3丁目4番10号
桜シール本社ビル

